コンパイラの処理としては通常、字句解析の次は構文解析を行います。
そこで、VBで基本的な構文解析を行ってみることにします。
実際に動くプログラムは、その44−VBでLL(1)構文解析サンプルにあります。
1. BNF記法 2. BNFと処理の関係 3. LL(1)構文解析器その問題点
4. ルールの修正 5. スタックを用いた構文解析 6. VBによる実装例
7. まとめ 参考文献
1. BNF記法
構文解析は、文法に沿って文を解析する処理です。
となると、文法をコンピュータが理解できるように表現しなければなりません。
プログラム言語の文法の表現にはBNF(Backus-Naur Form:Wikipediaの説明)記法がよく用いられます。
BNFでは、以下の形式のルール(生成規則)を並べて文法を表現します。
<X> := <A> | <B> | <C> | ... これは、「<X>は<A>または<B>または<C>または〜〜で定義される」ことを意味します。 <A>や<B>は複数の記号を羅列することができます。 例: <式> := <数値> | <式> + <式> | ( <式> ) この規則では、「式は、"1つの数値"か、"式+式"か"(式)"からなる」と読めます。 右辺にも<式>が出るように、再帰的な定義もできます。 |
この例に則ると、以下のいずれも式となります。
最後の2つは、定義を再帰的に適用した例です。
10 、 3 + 5 、 ( 20 ) 、 10 + (30 + 40) 、 ( (10 + 20) + 30) + ( 40 )
この中で10 + (30 + 40)がどのようにBNFから導けるか考えて見ます。
まず、「<式> := <数値>」のルールより、数値はそれだけで式になります。
ここでまず式 + ( 式 + 式 )となります。
次に、「<式> := <式> + <式>」のルールより、式と式の和も式なので、 式 + ( 式 ) になり、
「<式> := ( <式> )」のルールより、式をカッコでくくったものも式なので 式 + 式
そしてまた式同士の和なので最終的に式となります。
最初にBNF記法は文法を表すと書きましたが、逆にBNFで表せないものは文法エラーと言えます。
例えば、「1 +」や「5 + 6 )」は上記のルールをどう使っても式にならず文法エラーです。
2. BNFと処理の関係
さて、BNF記法を使うと、文法を表現できることがわかりました。
では、先ほどの10 + (30 + 40)がどのような構成をしているか、木構造で見てみます。
青矢印は<式> := <数値>、 赤矢印は<式> := <式> + <式> 黒矢印は<式> := ( <式> )のルールに対応しています。
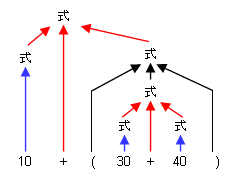
この構造がわかると、コンピュータが計算するための順序がわかります。
最終的に求めたいのは一番上、全体の式の値です。
そのためには、この木構造を下から辿り計算していけばよいことになります。
すなわち、BNF記法で示す文法に則って、プログラムからこの木構造を作り出すことができれば、プログラムの処理順序もわかると言えます。
これは単にこのような計算式だけではなく、if文やfor文についても同様です。
3. LL(1)構文解析器その問題点
さて、プログラムをコンパイルするためには、BNF記法に則って処理対象のプログラムを解析し、上の様な木構造を作らなければなりません。
これをどのようにコンピュータにやらせるか、というのが今回の本題になります。
種々の手法のうち、ここでは比較的単純なLL(1)構文解析という手法をVBで実装していきます。
LL(1)はお手軽な分それなりにデメリットもあり、解析できないルールがあります。
例えばXMLはLL(1)で解析できますが、C言語はLL(1)では解析できません。
LL(1)は簡単に言うと、「左から順に記号を読んでいって、行ける方向のルールを辿る」という方式です。
実は上の<式>のルールはLL(1)では解析できません。
例えば10 + ( 30 + 40 )を解析しようとする場合、最初の10だけみても、「<式> := <数値>」と「<式> := <式> + <式>」のどちらを適用した方がいいかは次の+をみるまで判断できません。
LL(1)で解析できないもう少しわかりやすい例として、VBのif文を考えて見ます。
if文にはelseがつく場合とつかない場合の2通りがあります。
<if文> := if <数値> then <処理> | if <数値> then <処理> else <処理>
さて、解析中ifが出てきた段階で、左右どちらのルールが適用できるか…を判定することはできません。
もう少し後ろまで探してelseがあるかどうかチェックすれば、判定は可能でしょう。
しかしLL(1)は「左から順に読む」方式であり、後ろのelseをみて行き先を決める、ということはできません。
どちらの例でも、解決法は2つあります。
・後ろの+やelseをみて判断するよう、もっと高度なアルゴリズムを使う。
・LL(1)で解析できるようルールを少し書き換える。
今回はLL(1)で行くと決めてしまったので、後者で行きます。
4. ルールの修正
さて、いきなりですが上の<式>の例を以下の様に書き換えました。
少し記号が複雑になっています。
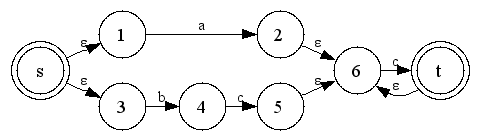
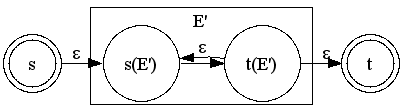
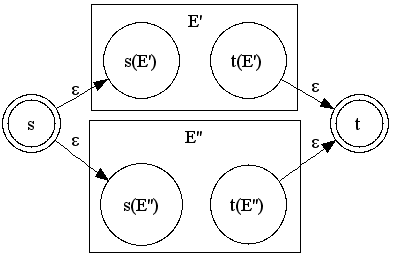
E -> T E' E' -> + T E' | # T -> ( E ) | id |
#というのは空文字、つまり何もないことの代用です。(一般にεで書かれることが多いですが、今回は#で。)
idというのは数値の変わりだと思ってください。
E、E'、Tの様にルールの左辺に来る記号を、非終端記号と呼びます。
(、)、#、idの様に、ルールの左辺に来ない記号を終端記号と呼びます。
終端記号は、実際に解析対象に現れる記号になります。
これで本当に前と同じ表現が可能か確認します。
まず、E -> T E'のE'を分配法則を使って展開すると、E -> T + T E' | Tになります。
さらにE'を展開するとE -> T + T E' | T + T | Tとなります。
以後これを繰り返すと、結局E -> T | T + T | T + T + T | T + T + T + T | …とT同士の和を取るものは、Tが何個あっても式になります。
さらにTは、idまたは括弧に囲まれた式Eを表すので、結果上に挙げたこれらの表記はいずれも式Eから導けることがわかります。
10 、 3 + 5 、 ( 20 ) 、 10 + (30 + 40) 、 ( (10 + 20) + 30) + ( 40 )
5. スタックを用いた構文解析
さて、LL(1)の説明に入って行きます。
入力10 + (30 + 40)を解析して、最終的に式Eとなることを示していきます。
LL(1)は以下の処理手順を取ります。
|
開始時、まずスタックには文末を示す記号$および最終的に求めたいもの(この場合E)を入れる。 また、入力の最後にも$を入れておく。 スタックの最上位の記号をX、入力の先頭をaとして、エラーまたは終了するまで以下の処理を繰り返し行う。
|
表M[X,a]というのは、「これから非終端文字列Xを解析するとき、入力が記号aだったらこのルールを適用する」というのが入っている表です。
この作り方はおいておいて、先ほどの式の例ではこの表は以下の様になります。
| + | # | ( | ) | id | $ | |
| E | E := T E' | E := T E' | ||||
| E' | E' := + T E' | E' := # | E' := # | |||
| T | T := ( E ) | T := id |
さて、これに則って10 + ( 30 + 40 )を解析してみます。
最初に数字は全部idに置き換えておきます。
| スタック | 入力 | 出力 | 解説 |
| $ E | id + ( id + id ) $ | ||
| $ E' T | id + ( id + id ) $ | (1) E := T E' | 2-aより、表M[E,id]をスタックに |
| $ E' id | id + ( id + id ) $ | (2) T := id | 2-aより、表M[T,id]をスタックに |
| $ E' | + ( id + id ) $ | 1-bより、スタックと入力を1つ取り除く | |
| $ E' T + | + ( id + id ) $ | (3) E' := + T E' | 2-aより、表M[E',+]をスタックに |
| $ E' T | ( id + id ) $ | 1-bより、スタックと入力を1つ取り除く | |
| $ E' ) E ( | ( id + id ) $ | (4) T := ( E ) | 2-aより、表M[T,(]をスタックに |
| $ E' ) E | id + id ) $ | 1-bより、スタックと入力を1つ取り除く | |
| $ E' ) E' T | id + id ) $ | (5) E := T E' | 2-aより、表M[E,id]をスタックに |
| $ E' ) E' id | id + id ) $ | (6) T := id | 2-aより、表M[T,id]をスタックに |
| $ E' ) E' | + id ) $ | 1-bより、スタックと入力を1つ取り除く | |
| $ E' ) E' T + | + id ) $ | (7) E' := + T E' | 2-aより、表M[E',+]をスタックに |
| $ E' ) E' T | id ) $ | 1-bより、スタックと入力を1つ取り除く | |
| $ E' ) E' id | id ) $ | (8) T := id | 2-aより、表M[T,id]をスタックに |
| $ E' ) E' | ) $ | 1-bより、スタックと入力を1つ取り除く | |
| $ E' ) | ) $ | (9) E' := # | 2-aより、表M[E',)]をスタックに ただし、E'は空文字なので実際はスタックには何も加えない。 |
| $ E' | $ | 1-bより、スタックと入力を1つ取り除く | |
| $ | $ | (10) E' := # | 2-aより、表M[E',)]をスタックに ただし、E'は空文字なので実際はスタックには何も加えない。 |
| 1-aより解析終了 |
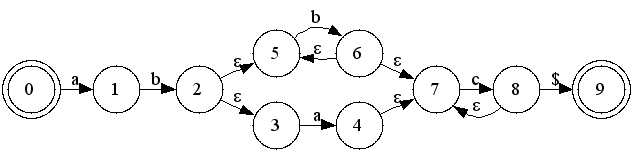
上の出力を順に適用して式Eを展開していくと、以下の図の様に確かに10 + ( 30 + 40 )が出来上がります。
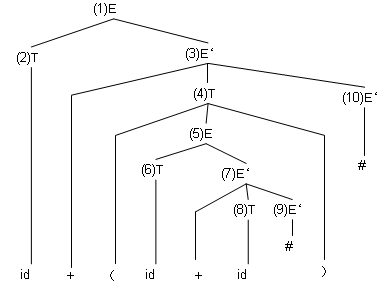
6. VBによる実装例
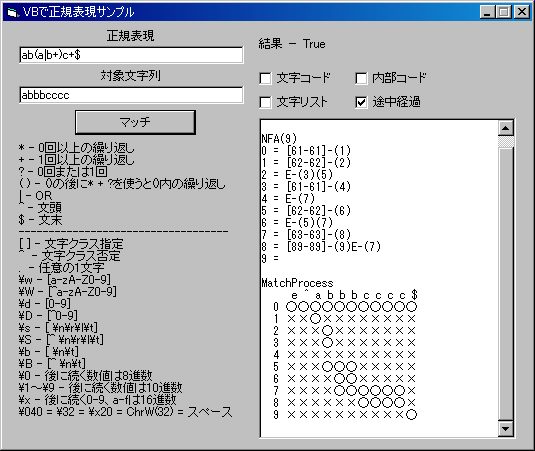
VB講座のその44−VBでLL(1)構文解析サンプルを利用すると、BNF文法と解析したい文字列を入れると表Mや解析結果を得ることができます。
(サイズの都合で、公開しているプログラムとボックスのレイアウトが異なります。)
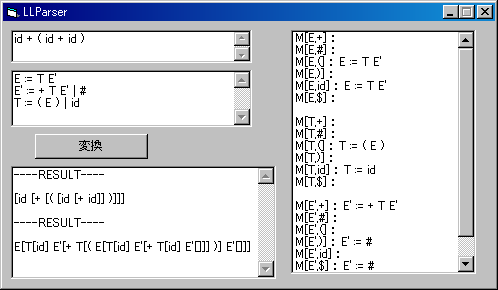
また、このプログラムの実際の構文解析のルーチンは以下の様になっています。
(一部エラー処理を削ってあります)
5.の処理手順と見比べると良いかも知れません。
'実際の構文解析
Public Function ParseTokenlist(P As Parser, StartSymbol As String, Tokenlist() As TokenCls) As TTNode
Dim TopNode As New TTNode
Dim BottomNode As New TTNode
Dim TmpNode As TTNode, TmpNode2 As TTNode
Dim Stack As New Collection
Dim i&, j&, Token As TokenCls
Dim prod As Production
Dim ni&, ti&
'スタックに初期値を積む
'文末記号をまずスタックに入れる
BottomNode.Label = "$"
Stack.Add BottomNode
'解析したいルールをスタックに入れる
TopNode.Label = StartSymbol
Stack.Add TopNode
Do
Set Token = Tokenlist(i) '現在の入力文字を取得
Set TmpNode = Stack(Stack.Count) 'スタックの最上位を取得
'終端記号の場合
If IsTerm(TmpNode.Label) Or TmpNode.Label = "$" Then
If TmpNode.Label = Token.Symbol Then
'スタックと入力が一致するなら、それぞれ1文字取り除く
i = i + 1 次の入力へ
Call Stack.Remove(Stack.Count)
Else
'エラー
Exit Function
End If
Else
'非終端記号の場合
'記号に対応する番号を取得
ni = IndexInCollection(TmpNode.Label, P.NontermList) - 1
If Token.Symbol = "$" Then
ti = P.TermList.Count
Else
ti = IndexInCollection(Token.Symbol, P.TermList) - 1
End If
'テーブルMを参照
prod = P.Table(ni, ti)
'テーブルが見つからない場合
If prod.NonTerm = "" Then
'エラー
Exit Function
End If
'X := Y1 Y2 Y3・・・に対して逆向きに積む
Call Stack.Remove(Stack.Count) 'まずXをどかす
If prod.SymbolList(0) <> "#" Then
'スタックに入れていく
For j = UBound(prod.SymbolList) To 0 Step -1
Set TmpNode2 = New TTNode
TmpNode2.Label = prod.SymbolList(j)
Call Stack.Add(TmpNode2)
Next
'この時点で出力にも積んでいく
For j = 0 To UBound(prod.SymbolList)
Call TmpNode.SubNode.Add(Stack(Stack.Count - j))
Next
End If
End If
Loop While i < UBound(Tokenlist)
Set ParseTokenlist = TopNode
End Function
|
7. まとめ
早足ですが、構文解析のためのBNF記法およびLL(1)文法を見ていきました。
しかしまだ課題は残っています。
「これから非終端文字列Xを解析するとき、入力が記号aだったらこのルールを適用する」という情報を持つ表Mの作り方が不明です。
次回、この表Mの作り方について見ていきます。
参考文献
- [1] A. V. エイホ, R. セシィ, J. D. ウルマン, 原田 賢一 『コンパイラI・II』サイエンス社, 1990年(amazon).
- [2] Wikipedia:LL parser.