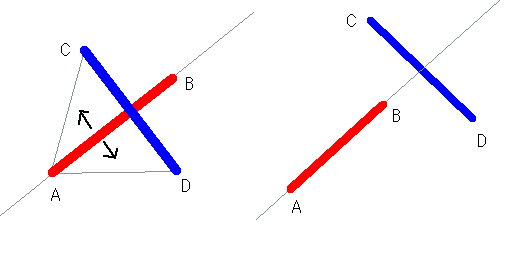
前回説明不足だった点もあるので、「直線」「線分」「半直線」の定義をあらかじめ確認しておきます。
(特に、「直線」と「線分」は使い分けてるので注意)
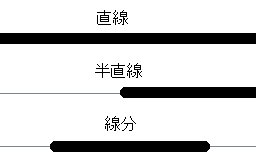
「直線」は無限に続きます。
「直線AB」はABを通り無限に(AやBの外側も)続きます。
「半直線」は1つだけ端があり、片方は無限に続きます。
「線分」は2つ端があり、有限です。
「線分AB」はAとBの間だけを指します。
「直線AB」と「線分AB」はABの外側も含むか含まないかが異なるので注意する必要があります。
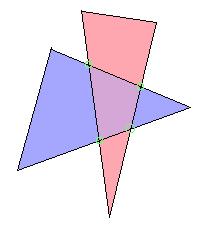
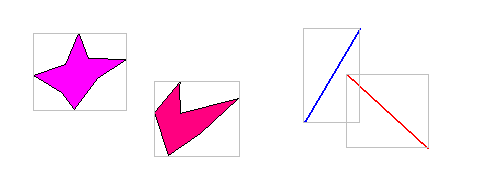
前回は多角形同士の交差判定の概要と、線分同士の交差判定を行いました。
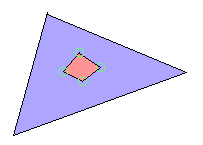
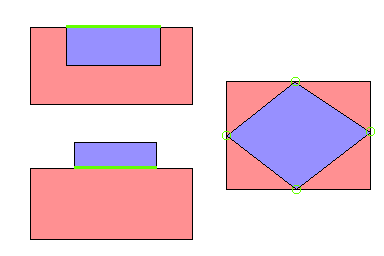
残るは、「小さい方(A)が完全に大きい方(B)に含まれる(A⊆B) → Aの各頂点がBに含まれる」の判定のみです。
実際はAの各頂点がBに含まれることをチェックしなくても1つでOKです。
1つの頂点が含まれてるなら他も全部Bに含まれてるはずなので。
(もしBに含まれないAの頂点がある場合、その頂点と内部の頂点を結ぶ線分がBの辺と交差するため、辺の交差判定の段階でチェック可能)
同様に、1つが外にあると全部外にあることになります。
まぁどちらにしても「ある点が多角形に含まれるかどうか?」を判定する必要があります。
ここでは、計算の手間と利用可能な条件の異なる3つの方法を紹介します。
先に3つの手法の違いを表にしときます。
| 手法の概要 | 計算速度 | 利用可能な条件 | |
| 手法1 | 各辺の内側にあることを判定 | 高速 | 凸多角形のみ |
| 手法2 | 点を通る半直線と境界の交差判定 | 中速(点の配置によって低速) | 特になし |
| 手法3 | 多角形の点と成す角の和の判定 | 低速 | 特になし |
各辺の内側判定による内外判定
前回の所で、外積を用いて直線の左側・右側を判定する手法を紹介しました。
これを利用して点の内外判定を行います。
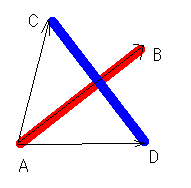
例えば、下のような例を考えるとわかりやすいかと思います。
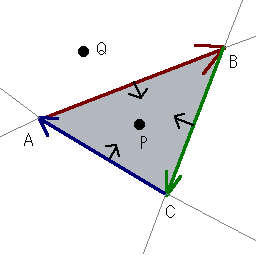
左の三角形の辺を、AB、BC、CAと右回りになるように辺を見ていきます。
三角形の中の点Pは、各辺の常に右側にあることがわかります。
点QはBC、CAの右側になってはいますが、ABの左側にあります。
逆にAC、CB、BAと左向きに回ったときは点Pは常に左側にあります。
要は、「辺をぐるっと回った時、常に点が同じ側にある→多角形の内側にある」と言うことが出来ます。
左の図の例では、点Pは右回りに辺を回った時常に右側にあります。
右回りに回った時に常に左側にある、と言う事はありえません。
上の図を見て、右回りに回った時常に左側に来るという領域は存在しない事がわかります。
そのため、実際は辺を左回りに辿ったか右回りに辿ったかは必要ありません。
常に同じ側にある、と言うことだけが重要です。
前回の外積を用いた左右判定を用いると、上の例では、(P-A)×(B-A)と(P-B)×(C-B)と(P-C)×(A-C)の符号が一致すればいい事になります。
0の場合は直線状にあると言うことなのでこれもOKです。
三角形でなく、四角形、五角形・・・となったときも判定する数が増えるだけです。
この手法は、引き算・掛け算・符号の判定だけで済むので非常に簡単です。
ただ、問題点として凸な図形にしか使えない点があります。
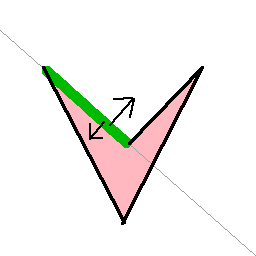
左の例では、太くなっている緑の辺の左右判定をした時、辺の両側に図形が存在します。
凸な場合は、常に同じ側で判定できましたが、凹な図形ではこの手法は使えません。
この場合は、図形をいくつかの凸な図形に分解するか、他の手法を使う必要があります。
この手法は他の手法に比べかなり計算が楽なので、凸な図形ならできるだけこの手法で行きたいところです。
境界との交差回数による内外判定
突然変な話ですが、団子に串を刺すことを考えてみます。
このとき各団子に対して串は「団子に入る・出る・入る・出る・・・」という順で刺さっていきます。
これと同じように、「点から半直線を伸ばし、多角形の境界との交差回数を調べる」という手法で判定が行えます。
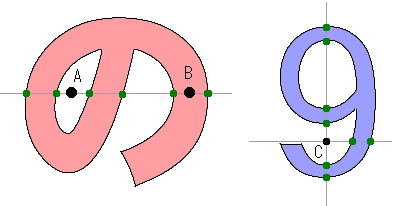
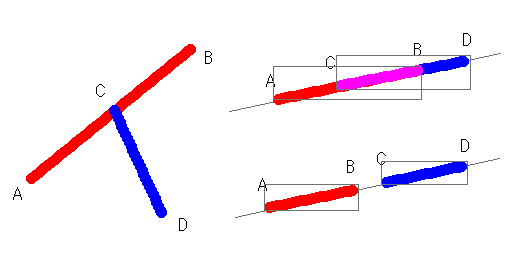
左側の図では「の」の字の近辺にある点A、Bが「の」の内側にあるかどうかを判定します。
A・Bの左側から串を刺したと想定します。(すなわち、点Aから左側に伸びた半直線と「の」の境界の交差回数を調べる。点Bから伸びる半直線についても同様。)
Aに到達する前には2回境界と交差します。Bの場合は5回ですね。
要は、「境界と奇数回交差しているならば内側」といえます。
「の」の例では求める点の左側での交差回数を調べましたが、別に右でも縦でも斜めでも構いません。
右の「9」の近辺にある点Cの例では上は4回、右と下は2回、左は0回交差していますが、いずれも偶数回=外側と判定されます。
上の図では「の」「9」と曲線の例を用いましたが、多角形の場合では多角形の各辺が(求めたい点から伸ばした)半直線と交差する回数を求める事になります。
ここで、別に斜めに延ばした線と各辺の交差判定をしても言いのですが、まぁ上下左右のいずれかだと判定がラクでしょう。
例えば、辺ABが求める点Pの左側に引いた半直線と交差するかどうかは以下の判定を順に行う事で簡単に求める事が出来ます。
|
文字で書くとわかりにくいですが、図を書いてみたりプログラム上で不等式を重い浮かべるとそれほどややこしい話ではありません。
線分(辺)と半直線(点まで刺した串)の交差判定だけだと簡単で済むのですが、残念ながらそうは行かない場合があります。
例えば、線分の両端のうち片方が半直線に重なったりすると下の図のようなことが発生します。
横方向の薄い灰色の線が半直線、太い黒線が多角形の一部と考えてください。(4つのパターンが書いてある図です)
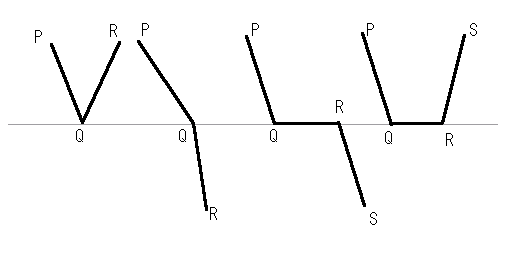
まず、左の2つはちょうど半直線と多角形の点Qが重なった場合です。
この例では、点Qの近辺で多角形の境界と半直線が交差しているか判断する事ができません。
次の点RがPと同じ側にあるか反対側にあるかを判定する必要があります。
一番左側のように点Pが上にある時、Qの次の点Rも上にあると、半直線と多角形は交差していないと考えられます。
2番目の例のようにRが下に来た場合は交差したと判定できます。
右の2つは半直線と辺QRが重なった場合です。
この場合は、PQが交差するか判定する場合Rまで見てもまだ交差するかしないか判定できません。
最終的に半直線から出る点Sまで調べる必要があります。
今回は、連続した辺が一直線に並んでないと仮定しています。(QRとRSは一直線に並ばない)
もし一直線に並ぶ可能性がある場合、R、Sと座標を見てもまだ交差するかどうかわからないので、さらに先の点を見る必要があります。
(さらに、当然QRが求める点の左側にあることを判定する必要があります。)
なお、「内外を求める点が辺QRの中に入っちゃったらどうするの?」という事が考えられますが、この場合は既に「辺同士の交差判定」の段階で判定されるので大丈夫です。
この手法は計算はそれほど大変ではないですが、このように図形の形によって多少余分な処理が入ります。
この手法はドーナツ型みたいに穴の空いた形でも利用可能です。
角度の和による内外判定
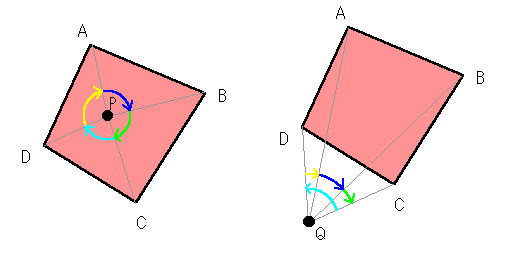
上の図で、調べたい点Pから多角形の点ABCDを順に見ていくとします。
この場合、A・B・C・D・Aと順に右回りに1周していることがわかると思います。
右の図では点Qに対して同じ事をやっていますが、こちらはA・B・Cと右に行った後、Dで左に戻り、また最後Aに戻る時に右に行ってます。
右向いて左向いて戻ってるだけで1周はしていません。
つまり、求めたい点Pに対して角度を∠APB+∠BPC+∠CPD+・・・と足した場合、内部にあれば1周するので360度(もしくは-360度)となり、外部にあれば0度になります。
(角度は符号付き、すなわち左回りと右回りは正負が異なると考える)
この手法は凸な図形でなくても使えるため、アルゴリズムとしてはわかりやすいです。
(凹な図形の場合、右回りの途中で少し左回りに戻ったりする事があるが、全体としては1周する)
もし点Pが辺AB上にのっていたりすると、∠APBが+180度なのか-180度なのか面倒なことが起こります。
しかしこの場合は、辺同士の交差判定の段階で交差しているとみなされるので、この処理を行う前に交差と判断されるので考える必要がありません。
(点Pが多角形の頂点に重なる場合も同様)
さて、あとは点A・B・Pがあったときに∠APBを符号も考えて求める方法がわかればいいということになります。
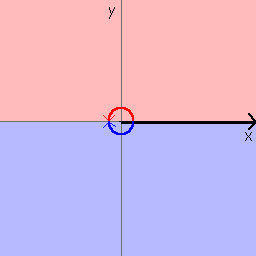
角度を求めるにはVBからはATan関数を使うしかないわけですが、そのためにはTan(∠APB)を求める必要があります。
その前に、VBのATan関数を拡張しておきます。
ATan関数はTanの値だけで判断するので、例えばTanθ=1となる場合でもθ=45度(第1象限)か225度(もしくは-135度、第3象限)か判断できない場合があります。
そのため、それも含めて値を返すATan2関数を定義しておきます。
定数0.001とか使ってるあたり適当ですが。
(C言語やJavaだと標準ライブラリでatan2があるんですけどね・・・)
Function Atan2(ByVal y As Double, ByVal x As Double) As Double '-PI〜PIの間の値を返す Dim t As Double If Abs(x) > 0.001 Then t = Atn(y / x) If x < 0 Then t = t + PI If t > PI Then t = t - 2 * PI Else If y > 0 Then t = PI / 2 If y < 0 Then t = -PI / 2 End If |
上の関数はyとxの値を入力するので第何象限にあるかも判断してくれます。
で、このyとxに対応する値を点A・B・Pからどう得るかという事になります。
このATan2を見ると、結局ATan2に入力しているのは、y=C sinθ、x=C cosθと結局sinとcosの値を入力しているに過ぎません。
で、sinとcosをどう求めるか・・・ですが、これはここまで出てきた話で解決できます。
ベクトルの外積でsin、内積でcosを求められます。
まとめると以下のようになります。
A' = A - P B' = B - P cos = A' ・ B' (内積) sin = A' × B' (外積) ∠APB = ATan2(sin,cos) |
内積や外積はいずれも直接cosやsinを求めるわけではなく、ベクトルの長さ|A'||B'|をかけた値が得られます。
ただ、ATan2でTanの値を一時的に計算する際に結局tan = sin / cosの計算をするので|A'||B'|は結局上下で打ち消し会うのでATan2に入れる前にベクトルの長さは考慮する必要はありません。
この角度計算を∠APB、∠BPC、∠CPD、・・・と行って足して行けば求められます。
この手法は図形が凹でも使えるし、上の手法みたく図形の形に依存しないのですが、ATanを使う事もあって結構計算量がかかるのが難点です。
また、この手法はそのままでは穴の空いた形には適用できません。
例えばドーナツ型の場合は外側の輪郭と内側の輪郭それぞれについて計算を行い、「外側の輪郭の内側で、かつ内側の輪郭の外側なら図形の内部」と判定する事になります。
プログラム側が「2つの輪郭からなる図形である」ということを知っていなければ行けません。
まとめ
前回は辺の交差判定、今回は点の内外判定についてまとめてみました。
辺の交差にしても点の内外判定にしても両方図形の点の数の積に比例した時間がかかります。
複雑な図形を直接判定するよりは、簡単な図形いくつかに分割した方がいいかも。
サンプルの方では一番最後の手法で実装しています。
今回は2次元での交差を扱いましたが、(具体的なアルゴリズムはともかく)アプローチは3次元(もしくはそれ以上)でも適用できます。
まず、辺同士の交差判定は言いかえれば境界同士が交差するかどうかの判定なので、3次元では面同士の交差判定をする事に相当します。
点の内外判定においても、
- 各点が各辺の内側にある→各点が各面の内側にある(ベクトル演算で計算可能)
- 点まで串を刺して辺との交差回数を計算→面との交差回数を計算
- 点を順に見てったとき1周するか計算→立体角で全方位分になるか(これはめんどうですね)